Intervals IV

Els intervals són molt útils per agrupar en conjunts i analitzar els nombres en la recta real. La seva importància recau a l'hora de construir funcions amb la precisió deguda.

Per estudiar els intervals es fa una introducció curta i acurada de les semirectes que són elements utilitzats per determinar més tard els intervals i altres productes amb més rigor.

Lògica d'intervals

En aquesta secció veurem com es treballen les condicions matemàtiques sobre la recta real. Concretament identificarem formes d'ajuntar condicions, escriure-les, descriure-les i representar-les matemàticament.

Les semirectes

A les matemàtiques quan utilitzem les següents condicions, suposicions o hipòtesis:

a<b,\;\;a>b,\;\;a\leqslant b,\;\;a\geqslant b

$a<b$

Es llegeix a és més petit que b, o inversament b és més gran que a.

$a>b$

Es llegeix a és més gran que b, o inversament b és més petit que a.

$a\leqslant b$

Es llegeix a és més petit o igual que b, o inversament b és més gran o igual que a.

Nota: dir "més petit o igual" vol dir que és cert tan si és més petit com si és més gran.

$a\geqslant b$

Es llegeix a és més gran o igual que b, o inversament b és més petit o igual que a.

Veiem exemples quan un dels dos és un nombre i detallem analitzant el seu significat dins la recta real.

Exemples

1.- Condició $x>10$

Diu que els valors de

x

han de ser valors més gran que 10.

Representació:

$10$
	$\;\;\;+\infty$

Descripció: S'assenyala en blau sobre la recta real els valors més grans que deu, però s'indica amb una rodona buida que no es vol assenyalar el deu, ja que el deu no pot ser més gran que deu i per tant no està dins dels possibles valors de

x.

Notació: $I=(10,\,+\infty )$

Lectura: Conjunt de tots els valors reals entre 10 i infinit positiu, amb el deu i l'infinit exclòs pels parèntesis. El seu nom és semirecta oberta.

2.- Condició $x\leqslant -3.$

Diu que els valors de

x

han de ser valor més petit o igual que -3.

Representació:

	$-3$
$-\infty \;\;\;$

Descripció: Aquesta representació assenyala els valors més petits que -3, i indica amb una rodona plena que el -3 també està dins dels possibles valors de

x.

Notació: $I=(-\infty ,\,-3]$

Lectura: Conjunt de tots els valors reals entre infinit negatiu i -3, amb el -3 inclòs amb la clau ]. El seu nom és semirecta tancada.

3.- Condició $x\geqslant -1.$

Significat: el valor de

x

pot ser un valor més gran o igual que -1.

Representació:

$-1$
	$\;\;\;+\infty$

Descripció: Aquesta representació assenyala els valors més grans que -1, i indica amb una rodona plena que el -1 també està dins dels possibles valors de

x.

Notació: $I=[-1,\,+\infty )$

Lectura: Conjunt de tots els valors reals entre -1 i infinit positiu, amb el -1 inclòs amb la clau [. El seu nom és semirecta tancada.

4.- Condició $x<7.$

Significat: el valor de

x

pot ser un valor més petit que 7.

Representació:

	$7$
$-\infty \;\;\;$

Descripció: Aquesta representació assenyala els valors més petits que 7, i indica amb una rodona buida que el 7 no està dins dels possibles valors de

x.

Notació: $I=(-\infty ,\,7)$

Lectura: Conjunt de tots els valors reals entre infinit negatiu i 7, amb el 7 exclòs amb el parèntesi ). El seu nom és semirecta oberta.

Exercicis

S'ha de representar i escriure la seva notació corresponent a cada apartat:

1) $x\leqslant 0.$

2) $x\geqslant -2.$

3) $x<4.$

4) $x>-3.$

Operacions

Les condicions bàsicament es poden combinar o agrupar de dos formes, o bé buscant coincidències o unint possibilitats. Ens interessa analitzar les conseqüències d'aquestes dues combinacions, per això utilitzarem dos operadors:

I=A\cap B,\;\;I=A\cup B

Mentre llegiu alguns exemples fixeu-vos en la propietat commutativa d'aquestes operacions, $I=A\cap B=B\cap A$ i $I=A\cup B=B\cup A$ :

Feu atenció, es pinta la part interior d'aquest "recipient" de nombres, és un contenidor on les vores s'han d'especificar bé si estan dintre o fora.

També hi ha "recipients" de nombres que no tenen que estar enganxats físicament.

Fora	Dins	Fora	Dins	Fora	Dins

Intersecció

Per fer una intersecció d'una condició A i amb una condició B només s'ha de indicar quins nombres compleixen les dues condicions a la vegada. Veiem exemples dels diferents producte de les possibles combinacions que es poden fer:

Exemples

1.- Suposem que $x<3$ i també afegim que $x>1,$ llavors, representarem sobre la recta només els valors que compleixen les dues condicions simultàniament es a dir:

$1$	$3$

Condicions: $A=(-\infty ,\,3)$ i $B=(1,\,+\infty )$

Operació intersecció: $I=$ $A\cap B=$ $(-\infty ,\,3)\cap (1,\,+\infty )$

Notació del resultat: $I=(1,\,3)$

Descripció de I: És literalment el conjunt de tots els valors entre l'1 i el 3, sense incloure aquests dos nombres. Són només els valors continguts dins de A i B a la vegada.

El seu nom és interval obert.

2.- Suposem que $x\leqslant 1$ i que $x>-2$ :

$-2$	$1$

Operació: $(-\infty ,\,1]\cap (-2,\,+\infty )$

Notació del resultat: $I=(-2,\,1]$

El seu nom és interval obert per l'esquerra i tancat per la dreta o interval semiobert.

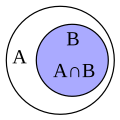
3.- Suposem que $x\leqslant 0$ i que $x<-5,$ llavors, representarem sobre la recta només els valors que compleixen les dues suposicions simultàniament es a dir:

	$-5$	$0$
$-\infty \;\;\;$

En aquest cas el que succeeix és que una intersecció d'un interval dintre d'un altre acaba guanyant el que sembla més petit.

Condicions: $A=(-\infty ,\,0]$ i $B=(-\infty ,\,-5)$

Operacions: $(-\infty ,\,0]\cap (-\infty ,\,-5)$

Notació del resultat: $I=(-\infty ,\,-5)$

Descripció de I: són tots els valors que estan dins dels dos conjunts a la vegada però resulta que B està totalment dins de A per tant el resultat és B, és a dir I=B.

4.- Suposem que $x\leqslant -1$ i que $x>3,$ llavors, representarem sobre la recta només els valors que compleixen les dues suposicions simultàniament es a dir:

$-1$	$3$

Les condicions inicials són contradictòries, per tant, no tenen cap coincidència i ens queda un conjunt sense nombres, és a dir, un conjunt buit i que evidentment no hem de pintar res.

Operació: $(-\infty ,\,-1]\cap (3,\,+\infty )$

Notació del resultat: $I=\{\emptyset \}=\emptyset$

El seu nom és conjunt buit.

5.- Suposem que $x\leqslant 9$ i que $x\geqslant 9,$ llavors, representarem sobre la recta només els valors que compleixen les dues suposicions simultàniament, és a dir:

9

La única coincidència es el 9, que és un punt fronterer, i per tant es l'únic element que compleix les dues condicions.

Operació: $(-\infty ,\,9]\cap [9,\,+\infty )$

Notació del resultat: $I=\{9\}$

El seu nom és punt o conjunt d'un sol element.

Unió

Per fer una unió de una condició A amb una condició B només s'ha de indicar que els diferents objectes estan junts encara que hi hagi forats, després només arreglem els trams superposats quan apareguin com a un de sol. Es proposa anar directament a la notació matemàtica per anar més ràpid.

Exemples

1.- Unió de semirectes: $A=(-\infty ,\,8)$ i $B=[9,\,\infty )$

Operació: $I=A\cup B=(-\infty ,\,8)\cup [9,\,\infty )$

Resultat: casualment queda igual per que no es pot arreglar més: $I=(-\infty ,\,8)\cup [9,\,\infty )$

Representació:

	8	9
$-\infty \;\;\;$			$\;\;\;+\infty$

Descripció: el resultat segueix sent dues semirectes.

2.- Unió de semirectes: $A=(-\infty ,\,-2)$ i $B=(-2,\,\infty )$

Operació: $I=A\cup B=(-\infty ,\,-2)\cup (-2,\,\infty )$

Resultat: veiem que és gairebé tota la recta real, excepte el -2, no es pot arreglar més: $I=(-\infty ,\,-2)\cup (-2,\,\infty )$

Representació:

	-2
$-\infty \;\;\;$		$\;\;\;+\infty$

Descripció: el resultat també son dues semirectes, però, vegeu que són tots els nombres reals sense un punt, el -2, es a dir, l'indicat amb una rodona buida.

3.- Unió de semirectes: $A=(-\infty ,\,10)$ i $B=(-9,\,\infty )$

Operació: $I=A\cup B=(-\infty ,\,10)\cup (-9,\,\infty )=\mathbb {R}$

Resultat: veiem que en ajuntar les dues semirectes no deixen cap forat, per tant el resultat es tots els nombres entre $-\infty$ i $\infty$ es a dir $\mathbb {R} .$

Representació i descripció: s'hauria de pintar tota la recta sense forats.

-\infty \;\;\;

\;\;\;+\infty

4.- Unió dels objectes A i B: $A=(0,\,2)\cup (4,\,6)$ i $B=[1,\,3]\cup [5,\,7]$

Operació: $I=(0,\,2)\cup (4,\,6)\cup [1,\,3]\cup [5,\,7]$

Resultat: $I=(0,\,3]\cup (4,\,7]$

Representació: només hem de pintar A i B, i veure que dona aquest resultat.

0	3	4	7

Exercicis

Busquem un valor que és major que deu i menor que catorze, o major que quinze i menor que setze. Representeu els valors acuradament.
Escriu la notació dels intervals representats a continuació:

-11	-10	-4	4	5	6	7	11

Resum lèxic

Noms apareguts sense matisar si és obert o tancat però que hem de conèixer:

Element (quan parlem de l'element més simples i indivisibles d'un conjunt)

Punt (quan ens referim a un únic nombre real com a element de la recta real, ...)

Conjunt (quan agrupem elements amb una finalitat definida)

Recta (quan ens referim a tota la recta real com a conjunt de nombres)
Semirecta (tots els punts de la recta que es troben a un mateix cantó d'un punt donat prèviament)
Interval (tots els nombres de la recta delimitada per altres dos punts)

Buit (que no hi ha res, cap element, cap nombre real,...)

Vegis també

Escola secundària

Matemàtiques 4 ESO

Notes i referències