En aquesta secció veurem la utilitat dels nombres enters i aprendrem a usar la seva notació correctament.
Exemples previs de nombres enters al nostre entorn:
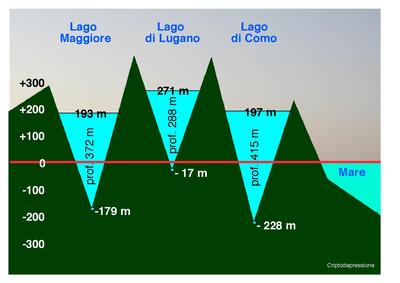
Mesura de la temperatura: el termòmetre i les línies isotèrmiques:
Mesura de l'alçaria respecte del nivell del mar:
L'ascensor: panell d'accés al aparcament.
Índex borsaris: Imatge fixa(no actualitzada).
Bolsa
Valor
Variación
Variación(%)
IBEX 35
8.924,00
-117,10
-1,29%
Futuros S&P 500
2.920,88
-16,62
-0,57%
Futuros Nasdaq
7.697,25
-42,75
-0,55%
Dow 30
26.478,02
-95,70
-0,36%
DAX
11.967,90
-129,53
-1,07%
Índice dólar
98,595
-0,070
-0,07%
Índice euro
95,89
+0,16
+0,16%
Futuros Bitcoin
8.190,0
-65,0
-0,79%
Per exemple nombres positius per un saldo i nombres negatius per indicar deutes. El contrari d'afegir o +1 és extreure o -1. El contrari de sumar o +1 és restar o -1. El contrari d'avançar o +1 és retrocedir o -1. I així successivament. Per construcció de la recta numèrica només cal dir que sempre els de la dreta són més grans que els de l'esquerra. Concretament:
Donat un número qualsevol, tot número situat a l'esquerra és més petit i tot número situat a la dreta és més gran.
Símbols per expressar o indicar l'ordre entre els nombres i particularment els enters:
El símbol següent entre les lletres
a
>
b
{\displaystyle a>b}
a és més gran que b ob és més petit que a .El símbol següent entre les lletres
a
<
b
{\displaystyle a<b}
a és més petit que b ob és més gran que a .El símbol següent entre les lletres
a
⩾
b
{\displaystyle a\geqslant b}
a és més gran que b i inclús podria ser igual ob és més petit que a i inclús podria ser igual.El símbol següent entre les lletres
a
⩽
b
{\displaystyle a\leqslant b}
a és més petit que b i inclús podria ser igual ob és més gran que a i inclús podria ser igual.La operació suma i resta com a notació signe usant la recta numèrica:
Exemple
a) +1+3-2+5-4=+3=3 b) +5-2-2-2=-1 c) -3+6-7+8-9=-5 d) -10+3+3+3+3=+2=2
e) -3-4-5-6-7=-25 f) -1+1-1+1-1+1-1+1=+0=0 g) -9+8+8-9=-2 h) -2+3+3-2+3+3-2=+6=6
Exercicis
1) -3-5+7-0 =
2) -7+6+0 =
3) -10+4-10+8-10+6 =
4*) 1-2+3-4+5-6+7-...+61-62 =
5) Un dofí dins del mar ascendeix 200 metres per caçar, després descendeix 400 metres tot seguit ascendeix 300 metres i, després de voltar, torna a ascendir 300 metres on roman quiet una estona i finalment ascendeix 200 metres arribant a la superfície del mar.
a) Feu un esquema ideal del recorregut del dofí. b) A quina profunditat es trobava inicialment? 6) Un ascensor avariat té adaptat un panell temporalment que no és gens adequat, llavors quan puja ho fa de 3 en 3, i quan baixa ho fa de 5 en 5. S'ha d'esbrinar la suma que dona el resultat demanat en aquest edifici com indica l'esquema:
🌞
+5
+4
+3
👫
+2
+1
🌲🌴
+0
🚗
-1
🏃
🧍
-2
a) Es vol pujar del pis -1 al pis 5e.
b) Es vol pujar del pis -2 al pis 5e.
a) Es vol baixar del 2n pis al 1r.
Aquesta taula s'ha de memoritzar, perquè serveix per multiplicar, dividir i simplificar parèntesis .
+
×
+
=
+
{\displaystyle +\times +=+}
−
×
+
=
−
{\displaystyle -\times +=-}
+
×
−
=
−
{\displaystyle +\times -=-}
−
×
−
=
+
{\displaystyle -\times -=+}
¿Per què serveix i on el veurem? Si tenim +15 € i es quadruplica, és a dir que es multiplica per 4, llavors fem (+15)⨯(+4)=+60 € i no hi ha més, no pot sortir negatiu. Si tenim un deute de -200 € i multipliquem aquest per 3, llavors el que volem fer és (-200)⨯(+3)=-600 que significa de tenim un deute i és de -600 € i l'ordre no importa també (+3)⨯(-200)=-600 € però ha de ser negatiu sinó vol dir que guanyem i això no pot ser. [ edit ] És freqüent trobar parèntesis amb un sol terme dins com -(-2), (-3), -(9) o (5), es pot interpretar com -(-2), +(-3), -(+9) o +(+5) respectivament ja que tot nombre sense signe és positiu.
Mètode de simplificació: s'identifiquen els signes de dins i de fora del parèntesis i es multipliquen amb la taula.Vegem-ho directament amb exemples explicats:
2)
−
(
+
(
−
9
)
)
{\displaystyle -{\Big (}+(-9)\;{\Big )}}
=
−
(
+
(
−
⏞
+
×
−
=
−
9
)
)
{\displaystyle =-{\Big (}\overbrace {+(-} ^{+\times -=-}9)\;{\Big )}}
=
−
(
−
9
)
{\displaystyle =-(-9)}
=
−
(
−
⏞
−
×
−
=
+
9
)
{\displaystyle =\overbrace {-(-} ^{-\times -=+}9)}
=
+
9
{\displaystyle =+9}
=
9
{\displaystyle =9}
3)
−
(
−
(
−
1
)
)
{\displaystyle -{\Big (}-(-1)\;{\Big )}}
=
−
(
−
(
−
⏞
−
×
−
=
+
1
)
)
{\displaystyle =-{\Big (}\overbrace {-(-} ^{-\times -=+}1)\;{\Big )}}
=
−
(
+
1
)
{\displaystyle =-(+1)}
=
−
(
+
⏞
−
×
+
=
−
1
)
{\displaystyle =\overbrace {-(+} ^{-\times +=-}1)}
=
−
1
{\displaystyle =-1}
Exercicis
1)
+
(
+
11
)
=
{\displaystyle +(+11)=}
2)
+
(
−
100
)
=
{\displaystyle +(-100)=}
3)
−
(
+
51
)
=
{\displaystyle -(+51)=}
4)
−
(
−
3
)
=
{\displaystyle -(-3)=}
5)
(
−
12
)
=
{\displaystyle (-12)=}
6)
(
2
)
=
{\displaystyle (2)=}
7)
−
(
8
)
=
{\displaystyle -(8)=}
8)
−
(
−
(
−
2
)
)
=
{\displaystyle -(-(-2))=}
Per multiplicar dos nombres enters només cal multiplicar els signes amb la taula i després multipliquem els nombres, vegem-ho amb exemples:
Exercicis:
1)
−
(
+
5
)
×
(
+
5
)
=
{\displaystyle -(+5)\times (+5)=}
2)
−
(
−
5
)
×
(
−
3
)
=
{\displaystyle -(-5)\times (-3)=}
3)
−
(
+
7
)
×
(
−
4
)
=
{\displaystyle -(+7)\times (-4)=}
4)
−
(
−
10
)
×
(
+
7
)
=
{\displaystyle -(-10)\times (+7)=}
5)
−
(
+
2
)
×
2
=
{\displaystyle -(+2)\times 2=}
6)
−
2
×
8
=
{\displaystyle -2\times 8=}
7)
−
4
×
(
−
5
)
=
{\displaystyle -4\times (-5)=}
8)
−
(
−
5
)
×
11
=
{\displaystyle -(-5)\times 11=}
En la divisió succeeix exactament el mateix, els signes es multipliquen i els nombres es divideixen com indica la operació, com per exemple:
Exercicis:
1)
−
(
+
100
)
÷
(
+
5
)
=
{\displaystyle -(+100)\div (+5)=}
2)
−
(
−
21
)
÷
(
−
3
)
=
{\displaystyle -(-21)\div (-3)=}
3)
−
(
+
64
)
÷
(
−
4
)
=
{\displaystyle -(+64)\div (-4)=}
4)
−
(
−
10
)
÷
(
+
2
)
=
{\displaystyle -(-10)\div (+2)=}
5)
−
100
÷
5
=
{\displaystyle -100\div 5=}
6)
−
(
−
21
)
÷
(
−
(
−
3
)
)
=
{\displaystyle -(-21)\div (-(-3))=}
7)
−
64
÷
(
−
4
)
=
{\displaystyle -64\div (-4)=}
8)
−
(
−
10
)
÷
2
=
{\displaystyle -(-10)\div 2=}
9) La temperatura d'un poble era 20 graus centígrads i es registres les següents variacions o oscil·lacions de temperatura fins a l'actualitat amb la taula:
a) -7
b) +6
c) -9
d) +10
e) -6
f) +5
g) -10
h) +11
Quina temperatura té actualment el poble? Ja havíem vist les potencies amb nombres naturals, es a dir amb els nombres
N
=
{
1
,
2
,
3
,
4
,
5
,
6
,
7
,
8
,
9
,
10
,
11
,
…
}
.
{\displaystyle \mathbb {N} =\{1,2,3,4,5,6,7,8,9,10,11,\dots \}.}
a
n
=
a
×
⋯
×
a
⏟
n
v
e
g
a
d
e
s
=
b
{\displaystyle a^{n}=\underbrace {a\times \dots \times a} _{n\;\;vegades}=b}
Per fer el mateix amb els enters només cal vigilar amb els nombres negatius, per exemple:
a)
(
−
2
)
1
=
(
−
2
)
=
−
2
{\displaystyle (-2)^{1}=(-2)=-2}
b)
(
−
3
)
2
=
(
−
3
)
×
(
−
3
)
{\displaystyle (-3)^{2}=(-3)\times (-3)}
=
+
3
×
3
{\displaystyle =+\;\;3\times 3}
=
+
9
=
9
{\displaystyle =+9=9}
c)
(
−
2
)
10
{\displaystyle (-2)^{10}}
=
(
−
2
)
×
(
−
2
)
×
(
−
2
)
×
(
−
2
)
×
(
−
2
)
×
(
−
2
)
{\displaystyle =(-2)\times (-2)\times (-2)\times (-2)\times (-2)\times (-2)}
×
(
−
2
)
×
(
−
2
)
×
(
−
2
)
×
(
−
2
)
{\displaystyle \times (-2)\times (-2)\times (-2)\times (-2)}
=
+
1024
{\displaystyle =+1024}
=
1024
{\displaystyle =1024}
d)
(
−
1
)
8
{\displaystyle (-1)^{8}}
=
(
−
1
)
×
(
−
1
)
⏟
+
×
(
−
1
)
×
(
−
1
)
⏟
+
×
(
−
1
)
×
(
−
1
)
⏟
+
×
(
−
1
)
×
(
−
1
)
⏟
+
{\displaystyle =\underbrace {(-1)\times (-1)} _{+}\times \underbrace {(-1)\times (-1)} _{+}\times \underbrace {(-1)\times (-1)} _{+}\times \underbrace {(-1)\times (-1)} _{+}}
=
(
+
1
)
×
(
+
1
)
×
(
+
1
)
×
(
+
1
)
{\displaystyle =(+1)\times (+1)\times (+1)\times (+1)}
=
+
1
{\displaystyle =+1}
=
1
{\displaystyle =1}
e)
(
−
1
)
9
{\displaystyle (-1)^{9}}
=
(
−
1
)
×
(
−
1
)
⏟
+
×
(
−
1
)
×
(
−
1
)
⏟
+
×
(
−
1
)
×
(
−
1
)
⏟
+
×
(
−
1
)
×
(
−
1
)
⏟
+
{\displaystyle =\underbrace {(-1)\times (-1)} _{+}\times \underbrace {(-1)\times (-1)} _{+}\times \underbrace {(-1)\times (-1)} _{+}\times \underbrace {(-1)\times (-1)} _{+}}
×
(
−
1
)
=
(
+
1
)
×
(
+
1
)
×
(
+
1
)
×
(
+
1
)
×
(
−
1
)
{\displaystyle \times (-1)=(+1)\times (+1)\times (+1)\times (+1)\times (-1)}
=
−
1
{\displaystyle =-1}
Així podem dir que:
(
−
a
)
n
=
(
−
a
)
×
⋯
×
(
−
a
)
⏟
n
v
e
g
a
d
e
s
=
a
n
=
+
b
=
b
{\displaystyle (-a)^{n}=\underbrace {(-a)\times \dots \times (-a)} _{n\;\;vegades}=a^{n}=+b=b}
n és parell
(
−
a
)
n
=
(
−
a
)
×
⋯
×
(
−
a
)
⏟
n
v
e
g
a
d
e
s
=
−
(
a
n
)
=
−
b
{\displaystyle (-a)^{n}=\underbrace {(-a)\times \dots \times (-a)} _{n\;\;vegades}=-(a^{n})=-b}
n és imparell o senar
Clarament el signe menys sobreviu només si l'exponent és imparell i per tant és en el que ens hem de fixar.
Exercicis de simplificació i càlcul
1)
(
−
2
)
5
=
{\displaystyle (-2)^{5}=}
2)
(
−
3
)
3
=
{\displaystyle (-3)^{3}=}
3)
(
−
5
)
2
=
{\displaystyle (-5)^{2}=}
4)
(
−
1
)
888
=
{\displaystyle (-1)^{888}=}
5)
(
−
1
)
999
=
{\displaystyle (-1)^{999}=}
6)
+
(
+
1
)
10
=
{\displaystyle +(+1)^{10}=}
7)
+
(
−
1
)
8
=
{\displaystyle +(-1)^{8}=}
8)
−
(
1
)
6
=
{\displaystyle -(1)^{6}=}
9)
−
(
−
1
)
22
=
{\displaystyle -(-1)^{22}=}
10)
−
(
−
2
)
7
=
{\displaystyle -(-2)^{7}=}
Com que ens agrada escriure pocs parèntesis, estem obligats a fer cas dels càlculs segons aquest ordre de prioritat:
1a) Els parèntesis . 2a) potencies . 3a) Productes i divisions. 4a) Sumes i restes. Per tant hem de fer amb prioritat unes operacions i després les de prioritat més baixa.
Exemples de productes i divisions amb sumes i restes:
Recordeu que primer es fan les multiplicacions o divisions i finalment quedarà una simple sèrie de sumes o restes.
Les multiplicacions i divisions successives es fan d'esquerra a dreta com es veu al apartat e :
a)
5
+
3
×
2
−
11
×
3
−
4
×
5
+
5
{\displaystyle 5+3\times 2-11\times 3-4\times 5+5}
=
5
+
3
×
2
⏞
−
11
×
3
⏞
−
4
×
5
⏞
+
5
{\displaystyle =5+\overbrace {3\times 2} -\overbrace {11\times 3} -\overbrace {4\times 5} +5}
=
5
+
6
−
33
−
20
+
5
{\displaystyle =5+6-33-20+5}
=
69
{\displaystyle =69}
b)
1
−
3
+
1
×
(
−
2
)
×
(
+
3
)
−
4
+
5
{\displaystyle 1-3+1\times (-2)\times (+3)-4+5}
=
1
−
3
+
1
×
(
−
2
)
×
(
+
3
)
⏞
−
4
+
5
{\displaystyle =1-3+\overbrace {1\times (-2)\times (+3)} -4+5}
=
1
−
3
+
(
−
6
)
−
4
+
5
{\displaystyle =1-3+(-6)-4+5}
=
−
7
{\displaystyle =-7}
c)
2
+
9
÷
3
−
3
÷
3
+
4
÷
2
−
8
{\displaystyle 2+9\div 3-3\div 3+4\div 2-8}
=
2
+
9
÷
3
⏞
−
3
÷
3
⏞
+
4
÷
2
⏞
−
8
{\displaystyle =2+\overbrace {9\div 3} -\overbrace {3\div 3} +\overbrace {4\div 2} -8}
=
2
+
3
−
1
+
2
{\displaystyle =2+3-1+2}
=
6
{\displaystyle =6}
d)
9
−
6
+
1
×
18
÷
3
÷
2
−
3
+
6
+
1
{\displaystyle 9-6+1\times 18\div 3\div 2-3+6+1}
=
9
−
6
+
1
×
18
÷
3
÷
2
⏞
−
3
+
6
+
1
{\displaystyle =9-6+\overbrace {1\times 18\div 3\div 2} -3+6+1}
=
9
−
6
+
3
−
3
+
6
+
1
{\displaystyle =9-6+3-3+6+1}
=
10
{\displaystyle =10}
e)
−
4
+
24
⋅
2
÷
4
÷
3
⋅
2
−
1
{\displaystyle -4+24\cdot 2\div 4\div 3\cdot 2-1}
=
−
4
+
24
⋅
2
⏟
÷
4
÷
3
⋅
2
⏞
−
1
{\displaystyle =-4+\overbrace {\underbrace {24\cdot 2} \div 4\div 3\cdot 2} -1}
=
−
4
+
48
÷
4
⏟
÷
3
⋅
2
⏞
−
1
{\displaystyle =-4+\overbrace {\underbrace {48\div 4} \div 3\cdot 2} -1}
=
−
4
+
12
÷
3
⏟
⋅
2
⏞
−
1
{\displaystyle =-4+\overbrace {\underbrace {12\div 3} \cdot 2} -1}
=
−
4
+
4
⋅
2
⏞
−
1
{\displaystyle =-4+\overbrace {4\cdot 2} -1}
=
−
4
+
2
−
1
{\displaystyle =-4+2-1}
Exemples de potències amb productes i divisions amb sumes i restes:
Sempre té prioritat l'exponent sobre la resta d'operacions o signes:
a)
9
+
3
2
=
9
+
3
2
⏞
=
9
+
9
=
18
{\displaystyle 9+3^{2}=9+\overbrace {3^{2}} =9+9=18}
b)
2
⋅
3
3
=
2
⋅
3
3
⏞
=
2
⋅
27
=
54
{\displaystyle 2\cdot 3^{3}=2\cdot \overbrace {3^{3}} =2\cdot 27=54}
c)
−
3
4
−
2
=
−
3
4
⏞
−
2
=
−
(
81
)
−
2
=
−
81
−
2
=
−
83
{\displaystyle -3^{4}-2=-\overbrace {3^{4}} -2=-(81)-2=-81-2=-83}
Exemples d'operacions amb parèntesis:
Els parèntesis són els constructors del nostre llenguatge matemàtic sense ells no podríem escriure
(
−
1
−
2
)
⋅
3
=
−
3
⋅
3
=
−
9
{\displaystyle (-1-2)\cdot 3=-3\cdot 3=-9}
−
1
−
2
⋅
3
=
−
1
−
6
=
−
7
,
{\displaystyle -1-2\cdot 3=-1-6=-7,}
(
−
2
)
4
=
+
16
=
16
{\displaystyle (-2)^{4}=+16=16}
−
2
4
=
−
16
{\displaystyle -2^{4}=-16}
a)
(
−
1
−
(
2
−
5
)
⋅
2
)
⋅
3
{\displaystyle (-1-(2-5)\cdot 2)\cdot 3}
=
(
−
1
−
(
2
−
5
)
⏞
⋅
2
)
⋅
3
{\displaystyle =(-1-\overbrace {(2-5)} \cdot 2)\cdot 3}
=
(
−
1
−
(
−
3
)
⋅
2
⏞
)
⋅
3
{\displaystyle =(-1\overbrace {-(-3)\cdot 2} )\cdot 3}
=
(
−
1
+
6
⏞
)
⋅
3
{\displaystyle =(\overbrace {-1+6} )\cdot 3}
=
5
⋅
3
{\displaystyle =5\cdot 3}
=
15
{\displaystyle =15}
b)
(
−
1
−
(
2
−
(
−
(
3
−
2
)
+
3
)
)
+
2
)
⋅
(
−
(
3
−
(
4
−
3
)
+
4
)
{\displaystyle (-1-(2-(-(3-2)+3))+2)\cdot (-(3-(4-3)+4)}
=
(
−
1
−
(
2
−
(
−
(
1
)
+
3
)
)
+
2
)
⋅
(
−
(
3
−
(
1
)
+
4
)
{\displaystyle =(-1-(2-(-(1)+3))+2)\cdot (-(3-(1)+4)}
=
(
−
1
−
(
2
−
(
−
1
+
3
)
)
+
2
)
⋅
(
−
(
3
−
1
+
4
)
)
{\displaystyle =(-1-(2-(-1+3))+2)\cdot (-(3-1+4))}
=
(
−
1
−
(
2
−
(
2
)
)
+
2
)
⋅
(
−
(
6
)
)
{\displaystyle =(-1-(2-(2))+2)\cdot (-(6))}
=
(
−
1
−
(
2
−
2
)
+
2
)
⋅
(
−
6
)
{\displaystyle =(-1-(2-2)+2)\cdot (-6)}
=
(
−
1
−
(
0
)
+
2
)
⋅
(
−
6
)
{\displaystyle =(-1-(0)+2)\cdot (-6)}
=
(
−
1
−
0
+
2
)
⋅
(
−
6
)
{\displaystyle =(-1-0+2)\cdot (-6)}
=
(
−
1
+
2
)
⋅
(
−
6
)
{\displaystyle =(-1+2)\cdot (-6)}
=
(
1
)
⋅
(
−
6
)
{\displaystyle =(1)\cdot (-6)}
=
−
6
{\displaystyle =-6}
Resta de seccions de primer d'ESO.