Introducció a les funcions IV

Des d'un punt de vista més rigorós, el tema de funció és semblant al que hem fet en altres temes i seccions. Una conseqüència discreta de les funcions és la representació gràfica en diverses matèries per fer estudi de dades en àrees molt concretes: productivitat, consum, natalitat, canvis de temperatura, preu dels productes, etc.

Les funcions a les matemàtiques és de gran utilitat per fer anàlisi rigorós del comportament de determinats successos, fins i tot, es poden fer estudis abstractes com a preludi elemental d'unes eines molt potents en cursos més avançats i on aquesta definició constaran com a assumides.

Aquesta secció està preparada per fer-se íntegrament o parcialment si ja s'ha fet el tema de funcion bàsiques

Definició de funció

La definició de les funcions a l'ESO només aconsegueix relacionar parells de nombres (x, y) al pla on usem coordenades, però, dos nombres x i y es considera un punt A = (x, y) , per tant, una funció establirà una serie de punts al pla deixant una mena de dibuix que es diu gràfic de la funció.

El primer conjunt de nombres és anomenat domini, X, i pot tenir la forma de recta real $\mathbb {R}$ , semirecta com $(-\infty ,\,a]$ o d'intervals.

El segon conjunt de nombres és anomenat recorregut (o imatge), Y.

Compta amb la restricció que fa la nostra definició de funció:

Definició: Una funció és una relació entre dos conjunts de nombres que donat un element x del primer anomenat domini, assignarà un únic element y numèric del segon conjunt anomenat recorregut.

Podem dir que $y=f(x)$ es pot entendre i llegir dient que podríem obtenir y fent diferents operacions amb la x.

Esquema per a funcions
${\begin{array}{rc}f:&X\to Y\\&\,x\mapsto y\end{array}}$	${\begin{array}{c}X{\xrightarrow {\;\;\;f\;\;\;}}Y\\\,x\mapsto y\end{array}}$

Notacions:

El nom d'una funció pot ser $f,g,h,i,\,...$ .

La $X$ majúscula indica el conjunt domini de la funció.

La $Y$ majúscula indica el conjunt recorregut de la funció.

Una taula de valors:

{\begin{array}{c|lr}x&y&=f(x)\\\hline a&1\\b&2\\c&3\\d&4\\\end{array}}

La representació es fa exactament igual com les equacions, partint de la taula de dos columnes obtenim els punts necessaris per fer la representació.

Exemples

1)

{\begin{array}{rccc}f:&X&{\xrightarrow {\;\;\;\;\;}}&Y\\&x&\mapsto &x-1\end{array}}

Taula:

{\begin{array}{c|c}x&f(x)\\\hline 0&-1\\1&0\\2&1\\3&2\\\vdots &\vdots \end{array}}

2)

{\begin{array}{rccc}f:&[0,\,1]&{\xrightarrow {\;\;\;\;\;}}&\mathbb {R} \\&x&\mapsto &2-x\end{array}}

Taula:

{\begin{array}{c|c}x&f(x)\\\hline 0&2\\0,1&1,9\\0,2&1,8\\0,3&1,7\\\vdots &\vdots \\1&1\end{array}}

3)

{\begin{array}{rccc}f:&(1,\,2)&{\xrightarrow {\;\;\;\;\;}}&\mathbb {R} \\&x&\mapsto &1\end{array}}

Taula:

{\begin{array}{c|c}x&f(x)\\\hline (1)&1\\1,1&1\\1,2&1\\1,3&1\\\vdots &\vdots \\(2)&1\end{array}}

4)

{\begin{array}{rccc}f:&[-1,\,0)&{\xrightarrow {\;\;\;\;\;}}&\mathbb {R} \\&x&\mapsto &-1\end{array}}

Taula:

{\begin{array}{c|c}x&f(x)\\\hline -1&-1\\-0,9&-1\\-0,8&-1\\-0,7&-1\\\vdots &\vdots \\(0)&-1\end{array}}

5)

{\begin{array}{rccc}f:&(-1,\,1]&{\xrightarrow {\;\;\;\;\;}}&\mathbb {R} \\&x&\mapsto &x^{2}\end{array}}

Taula:

{\begin{array}{c|c}x&f(x)\\\hline (-1)&1\\-0,5&0,25\\0&0\\0,5&0,25\\\vdots &\vdots \\1&1\end{array}}

6)

{\begin{array}{rccc}f:&[0,\,+\infty )&{\xrightarrow {\;\;\;\;\;}}&\mathbb {R} \\&x&\mapsto &{\sqrt {x}}\end{array}}

Taula:

{\begin{array}{c|c}x&f(x)\\\hline 0&0\\1&1\\4&2\\9&3\\\vdots &\vdots \end{array}}

7)

{\begin{array}{rccc}f:&[1,\,+\infty )&{\xrightarrow {\;\;\;\;\;}}&\mathbb {R} \\&x&\mapsto &{\cfrac {1}{x}}\end{array}}

Taula:

{\begin{array}{c|c}x&f(x)\\\hline 1&1\\2&0,5\\4&0,25\\5&0,2\\10&0,1\\\vdots &\vdots \end{array}}

Funcions definides a trossos

Per detallar una funció, es pot fer de forma més sintètica i reduïda, parlant només de $f(x)=...$ i, a continuació, el seu domini on es considera aquesta x.

Exemples

1) Funció que assigna 1 als nombres més petits que dos i assigna 0 als nombres més grans o iguals que dos.

f(x)={\begin{cases}1&{\text{ Si }}x<2\\0&{\text{ Si }}2\leq x\end{cases}}

2) Funció que assigna 0 als nombres més petits o igual que zero i també més grans que dos, assigna x als nombres entre zero i u,i assigna 2-x als nombres entre u i dos ambdós inclosos.

f(x)={\begin{cases}0&{\text{ Si }}x\leq 0{\text{ o }}2<x\\x&{\text{ Si }}0<x<1\\2-x&{\text{ Si }}1\leq x\leq 2\end{cases}}

3) Funció amb 7 parts?:

f(x)={\begin{cases}1+x&{\text{ Si }}0\leq x<1\\2&{\text{ Si }}1\leq x\leq 2\\x&{\text{ Si }}2<x\leq 3\\2x-3&{\text{ Si }}3<x<4\\21-4x&{\text{ Si }}4<x<5\\1&{\text{ Resta de cassos}}\end{cases}}

Funció valor absolut

De les més utilitzades en totes les àrees del coneixement.

f(x)=|x|={\begin{cases}-x&{\text{ si }}x<0\\x&{\text{ si }}0\leq x\end{cases}}

Vegem com és la taula per cada una de les dues excepcions:

{\begin{array}{c|c}x&-x\\\hline (0)&0\\-1&1\\-2&2\\-3&3\\\vdots &\vdots \end{array}}

{\begin{array}{c|c}x&x\\\hline 0&0\\1&1\\2&2\\3&3\\\vdots &\vdots \end{array}}

Observació

La distància o passa entre valors que anem provant és de una unitat: h = 1

Per fer detalls més delicats podem escollir valors més petits: h = 0,5

Si h és molt petit, llavors la taula serà molt gran i trigarem molt en omplir-la.

Exemple de passa h = 0,1:

{\begin{array}{c|c}x&|x|\\\hline 0&0\\0,1&0,1\\0,2&0,2\\0,3&0,3\\0,4&0,4\\0,5&0,5\\0,6&0,6\\0,7&0,7\\0,8&0,8\\0,9&0,9\\1&1\\\vdots &\vdots \end{array}}

Observeu que per representar el tros que va del zero a l'u hem fet massa càlculs per res. Pensem per tant en fer càlculs estratègicament situats per estalviar càlculs innecessaris.

Exemple de programa que representa el $\sin(x*60)$ amb diferents fragments nh=6 però que pot ser nh=9, nh=18 o nh=36.

Dibuix en format *.svg que inclou un miniprograma que representa funcions editant el codi.

Arxiu per copiar i desar amb el Bloc de notes: tipus *.*, format UTF-8 i un nom com Program.svg

<svg width="1000" height="1000" xmlns="http://www.w3.org/2000/svg" xmlns:xlink="http://www.w3.org/1999/xlink" onload="create(evt)">
<script><![CDATA[
var xmlns="http://www.w3.org/2000/svg";
var ax1=-3;ax2=6;axw=1000;by1=-7;by2=6;byw=1000;//Interval:X,(ax1,ax2), Y,(by1,by2).
var nh=6;//numero de pasos o fragmentos.
var Root=document.documentElement//Contenedor de elementos.
function create(){
 var vy;vx=ax1;h=(ax2-ax1)/nh;dim=axw/(ax2-ax1);//variables y ajuste del marco.
 var cadena="m";ejes="m";cuadri="";by2=by1+(ax2-ax1);//marco cuadrado.
G=document.createElementNS(xmlns,"g");Root.appendChild(G);G.setAttributeNS(null,"transform","scale("+(dim)+"),translate("+(-ax1)+","+(by2)+")");
 P=document.createElementNS(xmlns,"path");E=document.createElementNS(xmlns,"path");
 F=document.createElementNS(xmlns,"path");T=document.createElementNS(xmlns,"text");//creadores.

 vy=fx(vx);cadena=cadena+(vx)+","+(-vy)+"L";
 for(vx=vx+h;vx<ax2+h;vx=vx+h,cadena=cadena+" "){ vy=fx(vx);cadena=cadena+(vx)+","+(-vy);}

 ejes=ejes+(0)+","+(-by1)+"L"+(0)+","+(-by2)+"q0.05,0.3 0.1,0.4q-0.1,-0.1 -0.2,0q0.05,-0.1 0.1,-0.4";//eje y.
 ejes=ejes+"M"+(ax1)+","+(0)+"L"+(ax2)+","+(0)+"q-0.3,-0.05 -0.4,-0.1q0.1,0.1 0,0.2q0.1,-0.05 0.4,-0.1";//eje x.
 for(i=0;i<(ax2-ax1)+1 || i<(by2-by1)+1;i++){
  cuadri=cuadri+"M"+(Math.round(ax1-1)+i)+","+(-by1)+"L"+(Math.round(ax1-1)+i)+","+(-by2);
  cuadri=cuadri+"M"+(ax1)+","+(-Math.round(by1-1)-i)+"L"+(ax2)+","+(-Math.round(by1-1)-i);
 }
 T.setAttributeNS(null,"x",30);T.setAttributeNS(null,"y",150);T.setAttributeNS(null,"font-size","18pt");
 F.setAttributeNS(null,"d",cuadri);F.setAttributeNS(null,"stroke","#444");F.setAttributeNS(null,"opacity","0.3");
F.setAttributeNS(null,"stroke-width",0.03);F.setAttributeNS(null,"fill","none");G.appendChild(F);
 E.setAttributeNS(null,"d",ejes);E.setAttributeNS(null,"stroke","black");
E.setAttributeNS(null,"stroke-width",0.03);E.setAttributeNS(null,"fill","black");G.appendChild(E);
 P.setAttributeNS(null,"d",cadena);P.setAttributeNS(null,"stroke","#00f");P.setAttributeNS(null,"stroke-width",0.03);
P.setAttributeNS(null,"fill","none");G.appendChild(P);

 Msg=document.createTextNode(cuadri);T.appendChild(Msg);// G.appendChild(T);//sonda de cadena.
}//Para fOrmulas matemAticas: Math.sin(), Math.Cos(), ...

function fx(x){return Math.sin(x*3.14/3);}//<<---******FUNCIoN f a representar.*********

]]></script>
 <path d="m1,1h998v998h-998z" stroke="#f5f" stroke-width="2" fill="none"/>
</svg>

Funció part entera

També es pot fer una funció de cada tipus de aproximació:

La funció d'aproximació per truncament, més conegut com part entera:

f(x)=[x]

Taula per analitzar:

{\begin{array}{c|c}x&f(x)\\\hline \vdots &\vdots \\0,8&0\\0,9&0\\1&1\\1,1&1\\1,2&1\\\vdots &\vdots \end{array}}

No és una funció a trossos encara que estigui molt fragmentada.

Fem ara la funció d'aproximació per arrodoniment:

f(x)={\bar {x}}

Taula per analitzar:

{\begin{array}{c|c}x&f(x)\\\hline \vdots &\vdots \\0,3&0\\0,4&0\\0,5&1\\0,6&1\\0,7&1\\\vdots &\vdots \end{array}}

Tampoc és una funció a trossos encara que estigui molt fragmentada. En programació es pot trobar com: Math.round(x) en javaScript.

Anàlisi gràfic

Mitjançant l'anàlisi gràfic és quan podem comprendre amb més fidelitat el comportament de cada funció. Es demana molt aquest tipus d'apreciacions per poder assegurar que es segueix el contingut del tema per anar-hi més lluny en un futur.

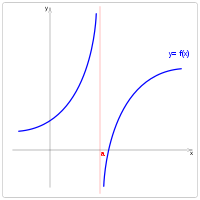
Continuïtat i discontinuïtat

La continuïtat o no d'una funció és el que el seu nom indica; només hem de comprovar que no hi ha salts al seu gràfic dins del seu domini. Per imaginar-ho, hem de pensar que:

Idealment una funció és continua quan es pot dibuixar el seu gràfic amb un llapis sense necessitat d'aixecar-lo del full.

Idealment una funció és discontinua quan no es pot dibuixar el seu gràfica amb un llapis sense aixecar-lo del full.

Exemples

1) Funció contínua:

2) Funció no contínua:

Creixement i decreixement

El creixement o decreixement només té sentit si sabem situar-nos, considerant que avancem pel gràfic anant en el sentit al infinit positiu.

Exemples

1) Creixement en una funció:

2) Decreixement en una funció:

Màxims i mínims

Parlem de màxims i mínims relatius(locals) quan analitzem un lloc concret del seu domini, per tant:

Es considera un màxim relatiu a un tros del domini quan és el punt més gran o més alt.

Es considera un mínim relatiu a un tros del domini quan és el punt més petit o més fondo.

Parlem de màxims i mínims absoluts(globals) quan es el punt més gran o més petit respectivament.

Simetries i periodicitat

Funció parella és la funció amb simetria vertical:

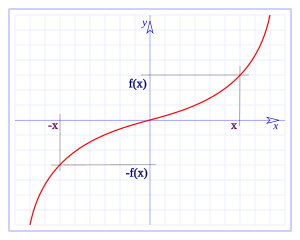
Funció imparella és la funció amb simetria central, és a dir, simetria respecte el punt O = (0, 0):

Funció periòdica és la funció que repeteix exactament i exclusivament una part concreta del seu gràfic al llarg del eix X:

Concavitat i Convexitat

Senzillament és com analitzar la curvatura d'una funció respecte l'horitzontal, si és un tros de $\cup$ es diu còncava i si és un tros de $\cap$ es diu convexa.

Nota: Aquesta nominació canvia quan estudiareu alguna especialitat, per tant es recomana seguir els apunts respectius.

Els punts de continuïtat que uneixen una corba convexa amb una corba còncava en l'ordre que sigui es diu punt d'inflexió. Exemples on s'indica el punt d'inflexió:

Trasllat de funcions

Per traslladar tots els punts d'una funció, necessitem un vector que ens digui el destí de tots els punts.

Dada la funció

f(x)

la seva funció traslladada amb el vector

{\vec {(a,b)}}

dona una funció:

g(x)=f(x-a)+b

Demostració:

Donada $f(x)$ els seus punts son de la forma $(x,f(x))$ i sumant el vector ${\vec {(a,b)}}$ dona:

(x,f(x))+{\vec {(a,b)}}=(x+a,f(x)+b)

El truc de canvi de variable $z=x+a$ i per tant $z-a=x$ per tant queda:

(x+a,f(x)+b)=(z,f(z-a)+b)

Finalment maquillant amb z=x tenim:

(x,f(x-a)+b)

És a dir $g(x)=(x,f(x-a)+b)$

Interpretació gràfica sobre taules, suposant que tenim la funció $f(x)=x^{2}$ , traslladar la funció ${\vec {(2,3)}}$ dona $g(x)=(x-2)^{2}+3$ :

{\begin{array}{c|c}x&f(x)\\\hline \vdots &\vdots \\-3&9\\-2&4\\-1&1\\0&0\\1&1\\2&4\\3&9\\\vdots &\vdots \end{array}}

{\begin{array}{c|c}x&g(x)\\\hline \vdots &\vdots \\-1&12\\0&7\\1&4\\2&3\\3&4\\4&7\\5&12\\\vdots &\vdots \end{array}}

Vigilem les taules comparant per columnes:

Veieu que la primera columna de la segona taula és la primera columna de la primera taula sumant 2 als seus valors.

Veieu que la segona columna de la segona taula és la segona columna de la primera taula sumant 3 als seus valors.

És una manera mólt ràpida de calcular-ho.

Exemples:

Tutorial per traslladar la funció $f(x)=|x|$ .

Trasllats i reflexions.

La primera part és interessant per $f(x)=(x)^{2}$ , la segona part fa comparatives per a qui interessi.

Funcions polinòmiques

Són funcions que es poden determinar mitjançant un polinomi com $f(x)=P(x)$ , és a dir si $P(x)=2x^{3}-x+3$ llavors:

f(x)=2x^{3}-x+3

{\begin{array}{rccc}f:&X&\xrightarrow {\;\;\;\;\;} &Y\\&x&\mapsto &2x^{3}-x+3\end{array}}

Taula:

{\begin{array}{c|c}x&2x^{3}-x+3\\\hline 0&2\cdot 0-0+3\\1&2\cdot 1-1+3\\\vdots &\vdots \end{array}}

Per tant si té taula llavors es pot representar.

A continuació es presenten les funcions ordenades segons el seu grau donant importància a aspectes visuals del seu gràfic.

Funcions de polinomis de grau 1 o menor

Són les funcions del tipus $f(x)=ax+b.$

Aquestes funcions són gràficament rectes al pla.

Classificació

Funció constant

Les funcions constants són del tipus $f(x)=b$ on b és un valor donat.

Exemples de funcions constants:

1) $f(x)=8$

2) $g(x)=4,2$

3) $h(x)=-3,6$

Visualment el seus gràfic de cadascuna és una única línia horitzontal

Funcions afins

Les funcions afins són del tipus $f(x)=ax+b$ amb $a\neq 0.$

Exemples de funcions afins:

1) $f(x)=2x+1$

2) $g(x)={\frac {x}{2}}+1$

3) $h(x)=-{\frac {x}{5}}+1$

Visualment el seu gràfic de cadascuna és una única línia de qualsevol mena a excepció de les línies verticals.

Funcions lineals

Les funcions lineals són del tipus $f(x)=ax,$ però és habitual trobar-les com $f(x)=ax+b$ degut al convenciment que el nom de lineal procedeix de ser línies rectes. En aquests casos es recomana seguir acuradament els textos donat pel docent concret.

Exemples de funcions lineals:

1) $f(x)=2x$

2) $g(x)={\frac {x}{2}}$

3) $h(x)=-{\frac {x}{5}}$

Determinació de la recta amb punts

Mètode punt a l'origen pendent

$f(x)={\frac {a}{b}}x+c$

Mètode dos punts lliures

$A=(a_{1},\;a_{2}),\;B=(b_{1},\;b_{2})$

${\frac {y-a_{2}}{x-a_{1}}}={\frac {b_{2}-a_{2}}{b_{1}-a_{1}}}$

O directament:

$f(x)={\frac {b_{2}-a_{2}}{b_{1}-a_{1}}}(x-a_{1})+a_{2}$

Funcions de polinomis de grau 2

Són les funcions del tipus $f(x)=ax^{2}+bx+c$ i afegirem les del tipus $f(x)=a(x+d)^{2}+e$ perquè comparteixen algunes característiques.

Exemple de efectes de variacions dels valors a, b i c. Per als valors de d i e de la segona expressió l'únic efecte que fan és desplaçar el vèrtex de la paràbola al punt (-d,e) i res més.